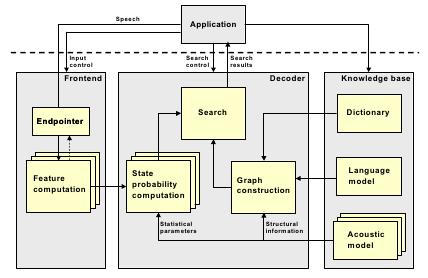
(originally posted at http://cmusphinx.sourceforge.net/2012/06/automating-the-creation-of-joint-multigram-language-models-as-wfst-part-2/)
Foreword
This a article presents an updated version of the model training application originally discussed in [1], considering the compatibility issues with phonetisaurus decoder as presented in [2]. The updated code introduces routines to regenerate a new binary fst model compatible with phonetisaurus’ decoder as suggested in [2] which will be reviewed in the next section.
1. Code review
The basic code for the model regeneration is defined in train.cpp in procedure
1 | void relabel(StdMutableFst *fst, StdMutableFst *out, string eps, string skip, string s1s2_sep, string seq_sep); |
where fst and out are the input and output (the regenerated) models respectively.
In the first initialization step is to generate new input, output and states SymbolTables and add to output the new start and final states [2].
Furthermore, in this step the SymbolTables are initialized. Phonetisauruss decoder requires the symbols eps, seq_sep, “<phi>”, “<s>” and “<s>” to be in keys 0, 1, 2, 3, 4 accordingly.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | void relabel(StdMutableFst *fst, StdMutableFst *out, string eps, string skip, string s1s2_sep, string seq_sep) { ArcSort(fst, StdILabelCompare()); const SymbolTable *oldsyms = fst->InputSymbols(); // Uncomment the next line in order to save the original model // as created by ngram // fst->Write("org.fst"); // generate new input, output and states SymbolTables SymbolTable *ssyms = new SymbolTable("ssyms"); SymbolTable *isyms = new SymbolTable("isyms"); SymbolTable *osyms = new SymbolTable("osyms"); out->AddState(); ssyms->AddSymbol("s0"); out->SetStart(0); out->AddState(); ssyms->AddSymbol("f"); out->SetFinal(1, TropicalWeight::One()); isyms->AddSymbol(eps); osyms->AddSymbol(eps); //Add separator, phi, start and end symbols isyms->AddSymbol(seq_sep); osyms->AddSymbol(seq_sep); isyms->AddSymbol("<phi>"); osyms->AddSymbol("<phi>"); int istart = isyms->AddSymbol("<s>"); int iend = isyms->AddSymbol("</s>"); int ostart = osyms->AddSymbol("<s>"); int oend = osyms->AddSymbol("</s>"); out->AddState(); ssyms->AddSymbol("s1"); out->AddArc(0, StdArc(istart, ostart, TropicalWeight::One(), 2)); ... |
In the main step, the code iterates through each State of the input model and adds each one to the output model keeping track of old and new state_id in ssyms SymbolTable.
In order to transform to an output model with a single final state [2] the code checks if the current state is final and if it is, it adds an new arc connecting from the current state to the single final one (state_id 1) with label “</s>:</s>” and weight equal to the current state’s final weight. It also sets the final weight of current state equal to TropicalWeight::Zero() (ie it converts the current state to a non final).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | ... for (StateIterator<StdFst> siter(*fst); !siter.Done(); siter.Next()) { StateId state_id = siter.Value(); int64 newstate; if (state_id == fst->Start()) { newstate = 2; } else { newstate = ssyms->Find(convertInt(state_id)); if(newstate == -1 ) { out->AddState(); ssyms->AddSymbol(convertInt(state_id)); newstate = ssyms->Find(convertInt(state_id)); } } TropicalWeight weight = fst->Final(state_id); if (weight != TropicalWeight::Zero()) { // this is a final state StdArc a = StdArc(iend, oend, weight, 1); out->AddArc(newstate, a); out->SetFinal(newstate, TropicalWeight::Zero()); } addarcs(state_id, newstate, oldsyms, isyms, osyms, ssyms, eps, s1s2_sep, fst, out); } out->SetInputSymbols(isyms); out->SetOutputSymbols(osyms); ArcSort(out, StdOLabelCompare()); ArcSort(out, StdILabelCompare()); } |
Lastly, the addarcs procuder is called in order to relabel the arcs of each state of the input model and add them to the output model. It also creates any missing states (ie missing next states of an arc).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | void addarcs(StateId state_id, StateId newstate, const SymbolTable* oldsyms, SymbolTable* isyms, SymbolTable* osyms, SymbolTable* ssyms, string eps, string s1s2_sep, StdMutableFst *fst, StdMutableFst *out) { for (ArcIterator<StdFst> aiter(*fst, state_id); !aiter.Done(); aiter.Next()) { StdArc arc = aiter.Value(); string oldlabel = oldsyms->Find(arc.ilabel); if(oldlabel == eps) { oldlabel = oldlabel.append("}"); oldlabel = oldlabel.append(eps); } vector<string> tokens; split_string(&oldlabel, &tokens, &s1s2_sep, true); int64 ilabel = isyms->AddSymbol(tokens.at(0)); int64 olabel = osyms->AddSymbol(tokens.at(1)); int64 nextstate = ssyms->Find(convertInt(arc.nextstate)); if(nextstate == -1 ) { out->AddState(); ssyms->AddSymbol(convertInt(arc.nextstate)); nextstate = ssyms->Find(convertInt(arc.nextstate)); } out->AddArc(newstate, StdArc(ilabel, olabel, (arc.weight != TropicalWeight::Zero())?arc.weight:TropicalWeight::One(), nextstate)); //out->AddArc(newstate, StdArc(ilabel, olabel, arc.weight, nextstate)); } } |
2. Performance – Evaluation
In order to evaluate the perfomance of the model generated with the new code. A new model was trained with the same dictionaries as in [4]
# train/train --order 9 --smooth "kneser_ney" --seq1_del --seq2_del --ifile cmudict.dict.train --ofile cmudict.fst
and evaluated with phonetisaurus evaluate script
# evaluate.py --modelfile cmudict.fst --testfile ../cmudict.dict.test --prefix cmudict/cmudict
Mapping to null...
Words: 13335 Hyps: 13335 Refs: 13335
######################################################################
EVALUATION RESULTS
----------------------------------------------------------------------
(T)otal tokens in reference: 84993
(M)atches: 77095 (S)ubstitutions: 7050 (I)nsertions: 634 (D)eletions: 848
% Correct (M/T) -- %90.71
% Token ER ((S+I+D)/T) -- %10.04
% Accuracy 1.0-ER -- %89.96
--------------------------------------------------------
(S)equences: 13335 (C)orrect sequences: 7975 (E)rror sequences: 5360
% Sequence ER (E/S) -- %40.19
% Sequence Acc (1.0-E/S) -- %59.81
######################################################################
3. Conclusions – Future work
The evaluation results in cmudict dictionary, are a little bit worst than using the command line procedure in [4]. Although the difference doesn’t seem to be important, it needs a further investigation. For that purpose and for general one can uncomment the line fst->Write(“org.fst”); in the relabel procedure as depicted in a previous section, in order to have the original binary model saved in a file called “org.fst”.
Next steps would probably be to write code in order to load the binary model in java code and to port the decoding algorithm along with the required fst operations to java and eventually integrate it with CMUSphinx.
References
[1] J. Salatas, “Automating the creation of joint multigram language models as WFST”, ICT Research Blog, June 2012.
[2] J. Salatas, “Compatibility issues using binary fst models generated by OpenGrm NGram Library with phonetisaurus decoder”, ICT Research Blog, June 2012.
[3] fstinfo on models created with opengrm
[4] J. Salatas, “Using OpenGrm NGram Library for the encoding of joint multigram language models as WFST”, ICT Research Blog, June 2012.